Understanding Dissociative Electron Attachment in Molecules: A Glimpse into Recent Advances

Dissociative Electron Attachment (DEA)

Dissociative Electron Attachment (DEA) is a pivotal process in molecular chemistry where an incoming low-energy electron attaches to a molecule, leading to its dissociation into fragments. This mechanism is crucial for understanding radiation damage in biological molecules, such as DNA, which can have significant implications for fields like biochemistry and medicine. Recent advancements were discussed at the 4th DEA Club Meeting in Potsdam, Germany, focusing on estimating DEA cross sections for various molecules, including carboxylic and amino acids. The below summarises the presentation of Dr Greg Armstrong in Potsdam.

Theoretical Framework and Computational Tools

Quantemol Electron Collisions (QEC) is a sophisticated computational tool that offers a user-friendly interface for calculating electron-molecule scattering cross sections. It integrates the Molpro quantum chemistry package to generate molecular target orbitals and employs the UKRmol+ code to compute these cross-sections using the R-matrix theory, a well-established method in quantum scattering calculations.

R-Matrix Theory,

The R-matrix theory divides space into three distinct regions:

Inner Region: Contains the N-electron molecular target where the incoming electron interacts with the molecule.
Outer Region: Here, the interactions of the outgoing electron with the inner electrons are considered negligible, simplifying the calculations.
Asymptotic Region: This region deals with the electron’s behaviour at large distances, focusing on the scattering effects.

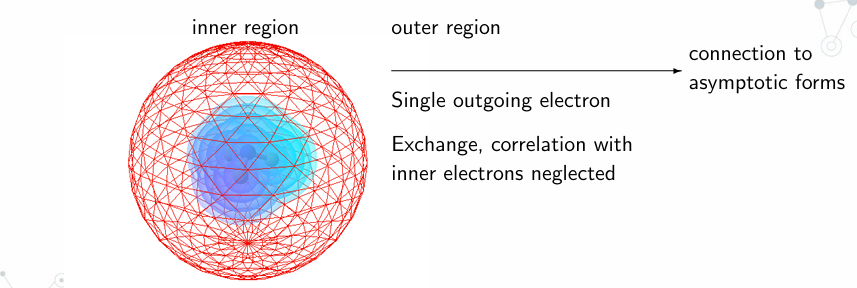
Figure 1: Schematic of the R-Matrix

The theory uses a time-independent Schrödinger equation for the (N+1)-electron system, solved via a wavefunction expansion, capturing the complexities of electron-molecule interactions.

The wavefunction expansion for the (N+1)-electron system is given by:

ψ_k^N+1 = A Σ _i,j c_ijk Φ_i^N(x₁, …, x_N) η_ij(x_N+1)+ Σ _m b_mk χ_m^N+1(x₁, …, x_N+1)

Calculating DEA Cross Sections

The DEA cross-section estimation involves determining the resonance energy (Er) and width (Γ) using the R-matrix method. The resonance cross section, σr(E), is calculated by integrating the product of the vibrational ground state wavefunction (Ψ(r)) and the Breit-Wigner cross section (σBW(E, r)). The Breit-Wigner formula characterizes the resonance features of the cross-section, essential for understanding the electron attachment and subsequent molecular dissociation.

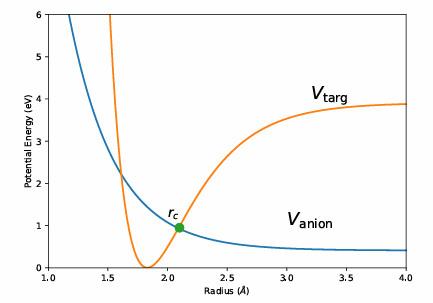
Figure 2: Graphical representation of DEA cross-section calculation

Formula:

σ_r(E) = ∫₀∞ Ψ*(r) σ_BW(E, r) Ψ(r) dr

σ_BW(E, r) = (2π / E) (1 / 4Γ²) [(E – V_r(Er, r))² + 1/4Γ²]

Where V_r(r) is the resonance potential, and the survival probability S is defined as:

S = e^-Γt

Where t is the time taken for the electron to reach a critical radius, r_c. The DEA cross-section for each resonance is then calculated as:

σ_DEA(E) = S σ_r(E)

Hydrogen Loss in Carboxylic and Amino Acids

A significant observation in DEA studies is the loss of hydrogen atoms from carboxylic and amino acids, forming (M – H)⁻ anions. This is predominantly due to π* shape resonances associated with the -COOH group. Accurately capturing these resonances is challenging and requires careful consideration of polarization effects, which are critical for precise resonance characterization.

Conclusion and Future Directions

The precise calculation of DEA cross-sections is vital for understanding the mechanisms of molecular damage, especially in biological contexts. The meeting underscored the importance of advanced computational tools like Quantemol and the need for further refinement in treating polarization effects, particularly for larger molecular systems. Future research aims to enhance these computational methods, potentially leading to better predictions of radiation effects on biological tissues and the design of molecules with specific properties.